 |
 |
|
 |
| EN |
|
Поиск по сайту
Авторизация
Подписка на новости
|
Закон Кулона
Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами. Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:
Иначе: Два точечных заряда в вакууме действуют друг на друга с силами, которые пропорциональны произведению модулей этих зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды. Эти силы называются электростатическими (кулоновскими). Важно отметить, что для того, чтобы закон был верен, необходимы:
Однако с некоторыми корректировками закон справедлив также для взаимодействий зарядов в среде и для движущихся зарядов. В векторном виде в формулировке Ш. Кулона закон записывается следующим образом: где Коэффициент kВ СГСЭ единица измерения заряда выбрана таким образом, что коэффициент k равен единице. В Международной системе единиц (СИ) одной из основных единиц является единица силы электрического тока ампер, а единица заряда — кулон — производная от него. Величина ампера определена таким образом, что k = c2·10-7 Гн/м = 8,9875517873681764·109 Н·м2/Кл2 (или Ф−1·м). В СИ коэффициент k записывается в виде: где В однородном изотропном веществе в знаменатель формулы добавляется относительная диэлектрическая проницаемость среды ε. В СГСЭ В СИ Закон Кулона в квантовой механикеВ квантовой механике закон Кулона формулируется не при помощи понятия силы, как в классической механике, а при помощи понятия потенциальной энергии кулоновского взаимодействия. В случае, когда рассматриваемая в квантовой механике система содержит электрически заряженные частицы, к оператору Гамильтона системы добавляются слагаемые, выражающие потенциальную энергию кулоновского взаимодействия, так, как она вычисляется в классической механике. Так, оператор Гамильтона атома с зарядом ядра Z имеет вид:
Здесь m — масса электрона, е — его заряд, Закон Кулона с точки зрения квантовой электродинамикиСогласно квантовой электродинамике, электромагнитное взаимодействие заряженных частиц осуществляется путём обмена виртуальными фотонами между частицами. Принцип неопределённости для времени и энергии допускает существование виртуальных фотонов на время между моментами их испускания и поглощения. Чем меньше расстояние между заряженными частицами, тем меньшее время нужно виртуальным фотонам для преодоления этого расстояния и следовательно, тем большая энергия виртуальных фотонов допускается принципом неопределенности. При малых расстояниях между зарядами принцип неопределённости допускает обмен как длинноволновыми, так и коротковолновыми фотонами, а при больших расстояниях в обмене участвуют только длинноволновые фотоны. Таким образом, с помощью квантовой электродинамики можно вывести закон Кулона. ИсторияВпервые исследовать экспериментально закон взаимодействия электрически заряженных тел предложил Г. В. Рихман в 1752—1753 гг. Он намеревался использовать для этого сконструированный им электрометр-«указатель». Осуществлению этого плана помешала трагическая гибель Рихмана. В 1759 г. профессор физики Санкт-Петербургской академии наук Ф. Эпинус, занявший кафедру Рихмана после его гибели, впервые предположил, что заряды должны взаимодействовать обратно пропорционально квадрату расстояния. В 1760 г. появилось краткое сообщениео том, что Д. Бернулли в Базеле установил квадратичный закон с помощью сконструированного им электрометра. В 1767 г. Пристли в своей «Истории электричества» отметил, что опыт Франклина, обнаружившего отсутствие электрического поля внутри заряженного металлического шара, может означать, что «электрическое притяжение следует точно такому же закону, как и тяготение, то есть квадрату расстояния». Шотландский физик Джон Робисон утверждал (1822), что в 1769 г. обнаружил, что шары с одинаковым электрическим зарядом отталкиваются с силой, обратно пропорциональной квадрату расстояния между ними, и таким образом предвосхитил открытие закона Кулона (1785). Примерно за 11 лет до Кулона, в 1771 г., закон взаимодействия зарядов был экспериментально открыт Г. Кавендишем, однако результат не был опубликован и долгое время (свыше 100 лет) оставался неизвестным. Рукописи Кавендиша были вручены Д. К. Максвеллу лишь в 1874 г одним из потомков Кавендиша на торжественном открытии Кавендишской лаборатории и опубликованы в 1879 г. Сам Кулон занимался исследованием кручения нитей и изобрел крутильные весы. Он открыл свой закон, измеряя с помощью них силы взаимодействия заряженных шариков. Закон Кулона, принцип суперпозиции и уравнения МаксвеллаЗакон Кулона и принцип суперпозиции для электрических полей полностью равносильны уравнениям Максвелла для электростатики Cтепень точности закона КулонаЗакон Кулона — экспериментально установленный факт. Его справедливость неоднократно подтверждалась всё более точными экспериментами. Одним из направлений таких экспериментов является проверка того, отличается ли показатель степени r в законе от 2. Для поиска этого отличия используется тот факт, что если степень точно равна двум, то поле внутри полости в проводнике отсутствует, какова бы ни была форма полости или проводника. Эксперименты, проведённые в 1971 г. в США Э. Р. Уильямсом, Д. Е. Фоллером и Г. А. Хиллом, показали, что показатель степени в законе Кулона равен 2 с точностью до Для проверки точности закона Кулона на внутриатомных расстояниях У. Ю. Лэмбом и Р. Резерфордом в 1947 г. были использованы измерения относительного расположения уровней энергии водорода. Было установлено, что и на расстояниях порядка атомных 10−8 см, показатель степени в законе Кулона отличается от 2 не более чем на 10−9. Коэффициент Поправки к закону Кулона в квантовой электродинамикеНа небольших расстояниях (порядка комптоновской длины волны электрона, где В сильных внешних электромагнитных полях, составляющих заметную долю от поля пробоя вакуума (порядка Закон Кулона и поляризация вакуумаЯвление поляризации вакуума в квантовой электродинамике заключается в образовании виртуальных электронно-позитронных пар. Облако электронно-позитронных пар экранирует электрический заряд электрона. Экранировка растет с ростом расстояния от электрона, в результате эффективный электрический заряд электрона где, — т. н. постоянная тонкой структуры — т. н. классический радиус электрона Эффект ЮлингаЯвление отклонения электростатического потенциала точечных зарядов в вакууме от значения закона Кулона известно как эффект Юлинга, который впервые вычислил отклонения от закона Кулона для атома водорода. Эффект Юлинга даёт поправку к лэмбовскому сдвигу 27 мггц. Закон Кулона и сверхтяжелые ядраВ сильном электромагнитном поле вблизи сверхтяжелых ядер с зарядом Значение закона Кулона в истории наукиЗакон Кулона является первым открытым количественным и сформулированным на математическом языке законом для электромагнитных явлений. С открытия закона Кулона началась современная наука об электромагнетизме. Источник: ru.wikipedia.org |
Читайте бесплатно
События из истории измерений
|
























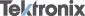




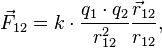
 — сила, с которой заряд 1 действует на заряд 2;
— сила, с которой заряд 1 действует на заряд 2; 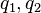 — величина зарядов;
— величина зарядов;  — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами —
— радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами —  );
);  — коэффициент пропорциональности. Таким образом, закон указывает, что одноимённые заряды отталкиваются (а разноимённые — притягиваются).
— коэффициент пропорциональности. Таким образом, закон указывает, что одноимённые заряды отталкиваются (а разноимённые — притягиваются).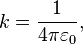
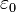 ≈ 8,854187817·10−12 Ф/м — электрическая постоянная.
≈ 8,854187817·10−12 Ф/м — электрическая постоянная.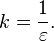

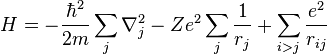 .
. — абсолютная величина радиус-вектора j-го электрона,
— абсолютная величина радиус-вектора j-го электрона,  . Первое слагаемое выражает кинетическую энергию электронов, второе слагаемое — потенциальную энергию кулоновского взаимодействия электронов с ядром и третье слагаемое — потенциальную кулоновскую энергию взаимного отталкивания электронов. Суммирование в первом и втором слагаемом ведется по всем N электронам. В третьем слагаемом суммирование идёт по всем парам электронов, причём каждая пара встречается однократно.
. Первое слагаемое выражает кинетическую энергию электронов, второе слагаемое — потенциальную энергию кулоновского взаимодействия электронов с ядром и третье слагаемое — потенциальную кулоновскую энергию взаимного отталкивания электронов. Суммирование в первом и втором слагаемом ведется по всем N электронам. В третьем слагаемом суммирование идёт по всем парам электронов, причём каждая пара встречается однократно. и
и  . То есть закон Кулона и принцип суперпозиции для электрических полей выполняются тогда и только тогда, когда выполняются уравнения Максвелла для электростатики и, наоборот, уравнения Максвелла для электростатики выполняются тогда и только тогда, когда выполняются закон Кулона и принцип суперпозиции для электрических полей.
. То есть закон Кулона и принцип суперпозиции для электрических полей выполняются тогда и только тогда, когда выполняются уравнения Максвелла для электростатики и, наоборот, уравнения Максвелла для электростатики выполняются тогда и только тогда, когда выполняются закон Кулона и принцип суперпозиции для электрических полей.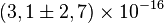 .
.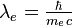 ≈3.86·10−13 м, где
≈3.86·10−13 м, где 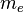 — масса электрона,
— масса электрона,  — постоянная Планка,
— постоянная Планка,  — скорость света) становятся существенными нелинейные эффекты квантовой электродинамики: на обмен виртуальными фотонами накладывается генерация виртуальных электрон-позитронных (а также мюон-антимюонных и таон-антитаонных) пар, а также уменьшается влияние экранирования (см. перенормировка). Оба эффекта ведут к появлению экспоненциально убывающих членов порядка
— скорость света) становятся существенными нелинейные эффекты квантовой электродинамики: на обмен виртуальными фотонами накладывается генерация виртуальных электрон-позитронных (а также мюон-антимюонных и таон-антитаонных) пар, а также уменьшается влияние экранирования (см. перенормировка). Оба эффекта ведут к появлению экспоненциально убывающих членов порядка 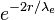 в выражении для потенциальной энергии взаимодействия зарядов и, как результат, к увеличению силы взаимодействия по сравнению с вычисляемой по закону Кулона. Например, выражение для потенциала точечного заряда
в выражении для потенциальной энергии взаимодействия зарядов и, как результат, к увеличению силы взаимодействия по сравнению с вычисляемой по закону Кулона. Например, выражение для потенциала точечного заряда  в системе СГС, с учётом радиационных поправок первого порядка принимает вид:
в системе СГС, с учётом радиационных поправок первого порядка принимает вид:
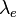 — комптоновская длина волны электрона,
— комптоновская длина волны электрона,  — постоянная тонкой структуры и
— постоянная тонкой структуры и  . На расстояниях порядка
. На расстояниях порядка 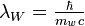 ~ 10−18 м, где
~ 10−18 м, где 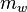 — масса W-бозона, в игру вступают уже электрослабые эффекты.
— масса W-бозона, в игру вступают уже электрослабые эффекты.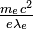 ~1018 В/м или
~1018 В/м или  ~109 Тл, такие поля наблюдаются, например, вблизи некоторых типов нейтронных звёзд, а именно магнитаров) закон Кулона также нарушается в силу дельбрюковского рассеяния обменных фотонов на фотонах внешнего поля и других, более сложных нелинейных эффектов. Это явление уменьшает кулоновскую силу не только в микро- но и в макромасштабах, в частности, в сильном магнитном поле кулоновский потенциал падает не обратно пропорционально расстоянию, а экспоненциально.
~109 Тл, такие поля наблюдаются, например, вблизи некоторых типов нейтронных звёзд, а именно магнитаров) закон Кулона также нарушается в силу дельбрюковского рассеяния обменных фотонов на фотонах внешнего поля и других, более сложных нелинейных эффектов. Это явление уменьшает кулоновскую силу не только в микро- но и в макромасштабах, в частности, в сильном магнитном поле кулоновский потенциал падает не обратно пропорционально расстоянию, а экспоненциально. является убывающей функцией расстояния
является убывающей функцией расстояния  . Эффективный потенциал, создаваемый электроном с электрическим зарядом
. Эффективный потенциал, создаваемый электроном с электрическим зарядом  , можно описать зависимостью вида
, можно описать зависимостью вида 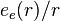 . Эффективный заряд
. Эффективный заряд 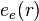 зависит от расстояния
зависит от расстояния  по логарифмическому закону:
по логарифмическому закону: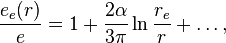
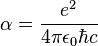
 ≈7.3·10−3;
≈7.3·10−3;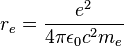
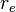 ≈2.8·10−13 см.
≈2.8·10−13 см. осуществляется перестройка вакуума, аналогичная обычному фазовому переходу. Это приводит к поправкам к закону Кулона.
осуществляется перестройка вакуума, аналогичная обычному фазовому переходу. Это приводит к поправкам к закону Кулона.

